Prof. Andriyan Bayu Suksmono, PhD.
School of Electrical Engineering and Informatics
Abstract
Finding Hadamard matrices is a computationally intensive problem due to the exponential growth of possible binary matrix configurations. This study explores a qubit-efficient method using Quantum Approximate Optimization Algorithm (QAOA) on universal quantum computers, bypassing the ancillary qubit needs of quantum annealers. Experiments demonstrate the ability to construct Williamson and Baumert-Hall Hadamard matrices of orders up to 132 with exponential performance improvement over random algorithms.
Keyword:QuantumSupremacy,QuantumUtility,MatriksHadamard,QAOA
Introduction
Hadamard matrices are orthogonal binary matrices with applications in communication systems, signal processing, and error correction. While low-order matrices can be constructed using classical methods, finding higher-order matrices is computationally intensive. The problem becomes infeasible for classical computing due to the exponential growth of orthogonality tests.
Quantum computing offers new possibilities for addressing such hard optimization problems. Quantum annealers have successfully found some high-order Hadamard matrices but require additional ancillary qubits, making scalability a challenge. This motivates the exploration of gate-based quantum computing, which eliminates ancillary qubit needs for multi-body interactions.
This paper investigates the use of QAOA for constructing Hadamard matrices on universal quantum computers. By employing QAOA, the computational complexity is significantly reduced, enabling the construction of large- order matrices. The research aims to demonstrate the feasibility and advantages of this approach compared to classical and quantum annealing methods.
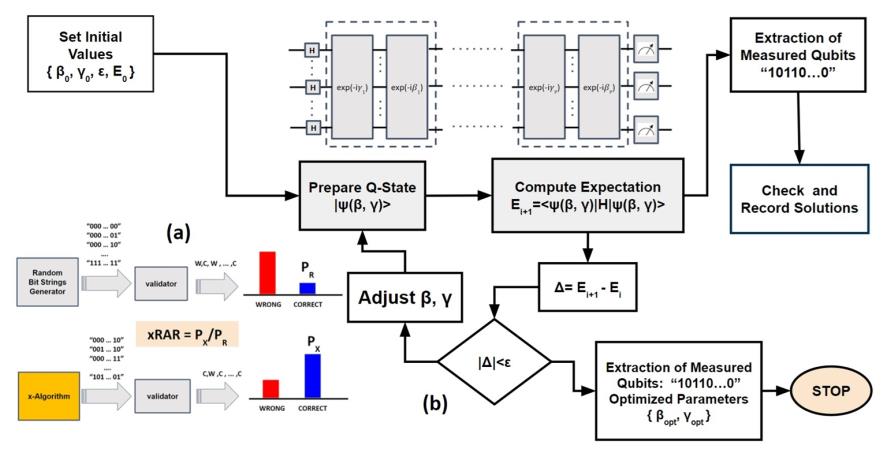
Research Method
Williamson and Baumert-Hall Methods
To reduce variable growth, the Williamson and Baumert-Hall methods decompose the problem into submatrices with complexity O(M), where M is the matrix order. These methods enable efficient matrix construction, avoiding the O(M^2) scaling of direct searches.
QAOA Framework
QAOA is based on a hybrid quantum-classical approach, where a problem Hamiltonian and a mixer Hamiltonian guide qubits to optimal configurations. The algorithm iteratively adjusts circuit parameters to minimize the cost function using classical optimizers.
Quantum Circuit Construction
Quantum circuits for 1- to 4-body interactions are designed using combinations of Z-rotation and CNOT gates. The circuits are implemented on IBM’s quantum simulator, capable of simulating up to 32 qubits. Cascaded circuit designs enable scalability for high-order problems.
Performance Metrics
The efficiency of QAOA is evaluated using the Quantum-to-Random Algorithm Ratio (QRAR), which compares the success rate of QAOA to that of a random search. Higher QRAR values indicate better algorithmic performance.
Experiment Setup
Experiments were conducted to construct Hadamard matrices of orders 44 and 132 using Williamson and Baumert-Hall methods. Simulations explored the impact of increasing circuit layers and qubit counts on performance, with optimizations performed using COBYLA. Figure 1 shows the experiment setup.
Discussion & Result
Experiments successfully identified Williamson Hadamard matrices of order 44 and Baumert- Hall matrices of order 132. The latter one is shown in Fig.2. The QAOA algorithm demonstrated exponential improvements in efficiency compared to random algorithms, with QRAR values approaching theoretical maxima.
Scalability was validated for problems with up to 24 qubits, showing consistent performance gains with increasing circuit layers. However, noise and complexity in higher-order searches revealed the need for improved quantum error mitigation techniques..

Conclusion
This study demonstrates the capability of QAOA to efficiently construct Hadamard matrices using universal quantum computers. By avoiding ancillary qubits, the method overcomes scalability challenges associated with quantum annealers, enabling the construction of larger matrices.
The experiments confirmed exponential performance improvements and validated the scalability of QAOA for higher-order matrix searches. These findings underscore the potential of gate-based quantum systems in addressing complex optimization problems.
Future work will focus on noise reduction, extending QAOA to unexplored matrix orders, and testing the approach on physical quantum hardware. This progress is expected to further solidify the role of quantum computing in solving previously intractable problems.